0. 들어가기 앞서

시스템 프로그래밍에 대해서 배우기 시작하면 연습 또는 과제로 흔히들 많이 푸는 것들이 있습니다. 컴공으로 세계 탑을 달리는 카네기멜론 대학교가 만든 DataLab, BombLab 등이 있습니다. 제가 공부했던걸 포스팅해 보도록 하겠습니다.

물론, 제가 푼 것이 모범답안은 아니고, 다소 귀찮게 푼 부분도 있으니 이렇게도 풀  수 있구나~ 이렇게 생각해 주시면 감사하겠습니다.

1. isAscii

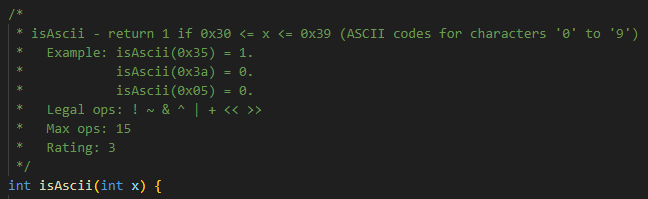
isAscii는 입력된 int형 변수 x의 값이 ascii 값으로 0~9, 즉 숫자이면 1을 반환하고, 그렇지 않다면 0을 반환하는 함수입니다. 허용된 operation에는 if문이 없으므로 shift 연산만을 이용하여 구현하면 됩니다.

int isAscii(int x) {
  int a = 255;
  int lb = 0;
  int ub = 0;
  int b = 0;
  int c = 0;
  a = (a << 8) + 255;
  a = (a << 8) + 255;
  lb = (a << 8) + 208;
  ub = (a << 8) + 198;
  b = (x + lb) >> 31;
  c = (x + ub) >> 31;
  return !(b) & c;
}

2. fourthBits

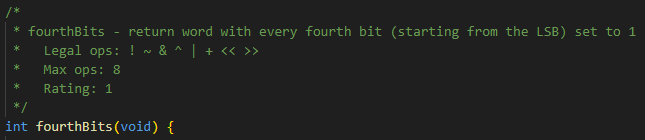
fourthBits 함수의 경우 32bit int형 데이터에서 4의 배수 위치에 있는 비트를 1로 바꾼 비트를 반환하면 됩니다. 숫자로 나타내면 아래와 같습니다.

00010001000100010001000100010001

int fourthBits(void) {
  int a = 17;
  a = (a << 8) + 17;
  a = (a << 8) + 17;
  a = (a << 8) + 17;
  return a;
}

3. countOneBits

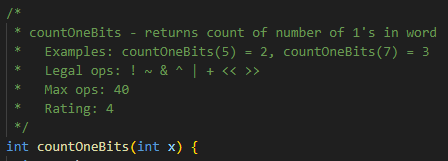
countOneBits는 word 사이즈의 데이터(4바이트)에 포함된 1의 갯수는 세는 함수입니다. 노가다하면 쉽게 해결할 수 있지만, Max ops가 40이므로 40번의 연산 내에 해결해야 합니다.

이를 위해서는 마스킹을 적절히 활용하면 연산 수를 줄일 수 있습니다. 병렬 비트 카운팅 기법(Parallel Bit Counting)을 활용하면 시프트 연산과 더하기를 이용하여 비트의 갯수를 셀 수 있습니다. 자세한 내용은 여기를 참고하세요.

저의 경우 다소 복잡하게 하였으니 위 링크 참고하셔서 더 짧게 만드실 수 있습니다.

int countOneBits(int x) {
  int mask1 = 85;
  int mask2 = 51;
  int mask3 = 15;
  int mask4 = 255;
  int mask5 = 255;
  int ones = 0;
  int a = 0;
  int b = 0;
  int c = 0;
  int d = 0;
  int e = 0;
  int f = 0;
  int g = 0;
  int h = 0;
  int i = 0;
  int j = 0;
  int k = 0;
  int l = 0;
  int m = 0;
  int n = 0;

  mask1 = (mask1 << 8) + 85;
  mask1 = (mask1 << 16) + mask1;
  mask2 = (mask2 << 8) + 51;
  mask2 = (mask2 << 16) + mask2;
  mask3 = (mask3 << 8) + 15;
  mask3 = (mask3 << 16) + mask3;
  mask4 = (mask4 << 16) + 255;
  mask5 = (mask5 << 8) + 255;

  a = x & mask1;
  b = (x >> 1) & mask1;
  c = a + b;
  d = c & mask2;
  e = (c >> 2) & mask2;
  f = d + e;
  g = f & mask3;
  h = (f >> 4) & mask3;
  i = g + h;
  j = i & mask4;
  k = (i >> 8) & mask4;
  l = j + k;
  m = l & mask5;
  n = (l >> 16) & mask5;
  ones = n + m;
  
  return ones;
}

4. countPattern

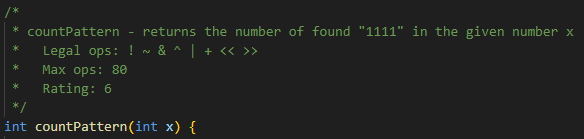
countPattern의 경우 어떤 int x를 받고, x의 binary에서 1111의 패턴이 몇 번 반복되는지 구하면 됩니다. 3번에서 사용한 mask를 적절히 이용하면 쉽게 해결할 수 있습니다.

int countPattern(int x) {
  int mask1 = 15;
  int mask2 = 1;
  int mask3 = 0;
  int initmask = 255;
  int a = 0;
  int b = 0;
  int c = 0;
  int d = 0;
  int e = 0;
  int f = 0;
  int g = 0;
  int h = 0;
  int temp = 0;
  int temp1 = 0;
  int patterns = 0;
  
  mask1 = (mask1 << 8) + 15;
  mask1 = (mask1 << 16) + mask1;
  mask2 = (mask2 << 8) + 1;
  mask2 = (mask2 << 16) + mask2;
  mask3 = mask2 << 4;

  a = x & mask1;
  b = (x >> 1) & mask1;
  c = (x >> 2) & mask1;
  d = (x >> 3) & mask1;
  e = (x >> 4) & mask1;
  f = (x >> 5) & mask1;
  g = (x >> 6) & mask1;
  h = (x >> 7) & mask1;

  a = a + mask2;
  a = a & mask3;

  b = b + mask2;
  b = b & mask3;

  c = c + mask2;
  c = c & mask3;

  d = d + mask2;
  d = d & mask3;

  e = e + mask2;
  e = e & mask3;

  f = f + mask2;
  f = f & mask3;

  g = g + mask2;
  g = g & mask3;

  h = h + mask2;
  h = h & mask3;

  temp = a + b + c + d + e + f + g + h;

  temp1 = (temp >> 4) + (temp >> 12) + (temp >> 20) + (temp >> 28);
  patterns = patterns + (initmask & temp1);
 
  return patterns;
}

5. subOverflowFree

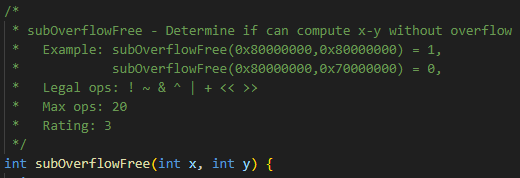
subOverflowFree 함수는 정수 x와 y를 받은 후, x-y 연산의 결과가 overflow를 일으키는지 체크하는 함수입니다. Overflow가 발생하면 0, 발생하지 않으면 1을 반환합니다.

int subOverflowFree(int x, int y) {
  int pos = 0;
  int a = 0;
  int xflag = 0;
  int yflag = 0;
  int sameflag = 0;
  int flag = 0;

  xflag = x >> 31;
  yflag = y >> 31;

  sameflag = xflag ^ yflag;

  pos = (~y) + 1;
  a = pos + x;
  flag = a >> 31;

  return !sameflag | !(flag ^ xflag);
}

6. mulSevenSixteenth

mulSevenSixteenth의 경우 어떤 정수 x를 받고, 7/16을 곱하는 연산을 한 후, overflow가 일어나지 않도록 rounding toward 0를 하면 됩니다.

int mulSevenSixteenth(int x) {
  int sign = 0;
  int a = 0;
  int b = 0;
  int mask = 255;
  int fmask = 15;
  int fsign = 0;

  sign = x >> 31;
  sign = sign & 1;

  a = x >> 8;
  b = x & mask;

  a = a + (a << 1) + (a << 2);
  b = b + (b << 1) + (b << 2);

  fsign = !(!(fmask & b));

  b = (b >> 4) + (a << 4) + (fsign & sign);
  return b;
}

7. sm2tc

sm2tc함수는 어떤 정수 x를 받은 후, 해당 x를 sign-magnitude 형식으로 변환한 후 반환합니다. Sign-magnitude 방식은 MSB를 부호 비트로 사용하며, MSB를 제외한 나머지 비트는 two’s complement로 크기를 나타내고, MSB로 부호를 나타내는 방식입니다.

int sm2tc(int x) {
  int a = 1;
  int sign = 0;
  int b = 0;

  a = a << 31;

  sign = x >> 31;
  
  b = (~x) + a + 1;
  return (sign & b) + ((~sign) & x);
}

8. float_abs

float_abs 함수는 input으로 float 형식으로 표현되어 있는 unsigned 값을 받습니다. 해당 float 값의 절댓값에 해당하는 float 형식의 unsigned를 반환하면 됩니다.

NaN인 경우만 제외해주고 부호 비트만 0으로 만들어 주면 되는 생각보다 간단한 task입니다. 또한, 이제부터는 if, while과 같이 모든 operation을 사용할 수 있습니다.

unsigned float_abs(unsigned uf) {
  int nan = 255;
  int a = 0;
  int mask = 128;

  a = uf << 1;
  mask = mask << 24;
  mask = ~mask;
  nan = (nan << 24);

  if ((a > nan) && (a < 0)) {
    return uf;
  } else {
    return mask & uf;
  }
}

9. integer_to_float

integer_to_float는 정수 x를 받은 후, 해당 정수 x와 equivalent한 float 형식을 unsigned로 반환하면 됩니다.

unsigned integer_to_float(int x) {
  unsigned int a = 0;
  unsigned int b = 0;
  unsigned int num = 0;
  unsigned int signflag = 0;
  unsigned int fracflag = 0;
  unsigned int final = 0;
  unsigned int exp = 0;
  int move = 0;
  unsigned int compmask = 0;
  unsigned int add = 0;
  unsigned int updownflag = 0;
  unsigned int processed = 0;

  if (x == 0) {
    return 0;
  }

  if (x == 0x80000000) {
    return 0xcf000000;
  }

  compmask = 0x80000000;
  fracflag = 0x007fffff;
  signflag = x & 0x80000000;
  if (signflag > 0) {
    a = (~x) + 1;
  } else {
    a = x;
  }

  b = a;
  processed = a;
  while (a != 0) {
    num = num + 1;
    a = a >> 1;
  }
  exp = 126 + num;
  move = num - 24;
  if (move > -1) {
    if (move > 1) {
      b = b << (32 - move);
      if (b > compmask) {
        add = 1;
      } else if (b == compmask) {
        updownflag = 1;
      }
    } else if (move == 1) {
      if (b & 1) {
        updownflag = 1;
      }
    }
    processed = processed >> move;
  } else {
    processed = processed << (24 - num);
  }
  processed = processed & fracflag;
  processed = processed + (updownflag & processed) + add;
  final = signflag + (exp << 23) + processed;
  return final;
}

10. real_quarter

real_quarter 함수는 float 형식으로 표현된 unsigned를 받고, 해당 float 값의 1/4을 float로 표현된 unsigned로 반환하면 됩니다.

Float에서 normalized와 denormalized 사이의 transition만 잘 고려해준다면 큰 무리없이 풀 수 있는 문제입니다.

unsigned real_quarter(unsigned uf) {
  unsigned int nan = 255;
  unsigned int expmask = 0;
  unsigned int fracmask = 0;
  unsigned int signmask = 0;
  unsigned int sign = 0;
  unsigned int exp = 0;
  unsigned int frac = 0;
  unsigned int updown = 0;
  unsigned int add = 0;
  unsigned int final = 0;
  
  nan = (nan << 24);
  if (uf > nan) {
    return uf;
  }

  if (uf == 0) {
    return 0;
  }

  if (uf == 0x80000000) {
    return uf;
  }

  signmask = 0x80000000;
  expmask = 0x7f800000;
  fracmask = 0x007fffff;
  
  sign = signmask & uf;
  exp = (expmask & uf) >> 23;
  frac = fracmask & uf;

  if (exp == 255) {
    return uf;
  } else if (exp > 1) {
    exp = exp - 2;
  } else if (exp > 0) {
    exp = 0;
    updown = frac & 0x00000003;
    frac = (frac >> 2) + 0x00200000;
  } else {
    updown = frac & 0x00000003;
    frac = frac >> 2;
  }
  if (updown > 2) {
    add = 1;
  } else if (updown == 2) {
    add = frac & 1;
  }

  final = sign + (exp << 23) + frac + add;
  return final;
}